To write the equation of a plane in 3D space, we need a point on the plane and a vector normal (orthogonal) to the plane. Page 10. 10. Example 4: Find the
18 pages
44 KB – 18 Pages
PAGE – 1 ============
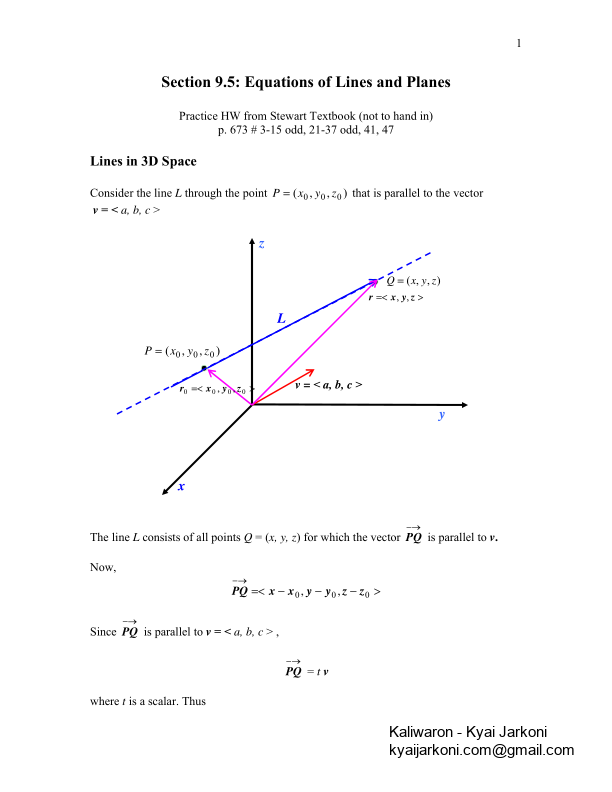
1Section 9.5: Equations of Lines and Planes Practice HW from Stewart Textbook (not to hand in) p. 673 # 3-15 odd, 21-37 odd, 41, 47 Lines in 3D Space Consider the line L through the point ) ,,(000zyxP that is parallel to the vector v = < a, b, c > The line L consists of all points Q = (x, y, z) for which the vector PQ is parallel to v. Now, 000,,zzyyxxPQ Since PQ is parallel to v = < a, b, c > , PQ = t v where t is a scalar. Thus x y ),,(000zyxP ),,(zyxQ z v = < a, b, c > L 0000,,zyxrzyxr,,
PAGE – 2 ============
2PQzzyyxx000,, = t v = < t a, t b, t c > Rewriting this equation gives cbatzyxzyx,,,,,,000 Solving for the vector zyx,, gives cbatzyxzyx,, ,,,,000 Setting r = zyx,,, 0r000,,zyx, and v = < a, b, c >, we get the following vector equation of a line. Vector Equation of a Line in 3D Space The vector equation of a line in 3D space is given by the equation 0rr t v where 0r = 000,,zyx is a vector whose components are made of the point ),,(000zyx on the line L and v = < a, b, c > are components of a vector that is parallel to the line L. If we take the vector equation cbatzyxzyx,, ,,,,000 and rewrite the right hand side of this equation as one vector, we obtain tcztbytaxzyx000,,,, Equating components of this vector gives the parametric equations of a line.
PAGE – 3 ============
3 Parametric Equations of a Line in 3D Space The parametric equations of a line L in 3D space are given by tczztbyytaxx000 , ,, where ),,(000zyx is a point passing through the line and v = < a, b, c > is a vector that the line is parallel to. The vector v = < a, b, c > is called the direction vector for the line L and its components a, b, and c are called the direction numbers. Assuming 0 ,0 ,0cba, if we take each parametric equation and solve for the variable t, we obtain the equations czztbyytaxxt000 , , Equating each of these equations gives the symmetric equations of a line . Symmetric Equations of a Line in 3D Space The symmetric equations of a line L in 3D space are given by czzbyyaxx000 where ),,(000zyx is a point passing through the line and v = < a, b, c > is a vector that the line is parallel to. The vector v = < a, b, c > is called the direction vector for the line L and its components a, b, and c are called the direction numbers. Note!! To write the equation of a line in 3D space, we need a point on the line and a parallel vector to the line.
PAGE – 5 ============
5Example 2: Find the parametric and symmetric equa tions of the line through the points (1, 2, 0) and (-5, 4, 2) Solution: To find the equation of a line in 3D space, we must have at least one point on the line and a parallel vector. We already have two points on e line so we have at least one. To find a parallel vector, we can simplify ju st use the vector that passes between the two given points, which will also be on this line. That is, if we assign the point P = (1, 2, 0) and Q = (-5, 4, 2), then the parallel vector v is given by 2 ,2 ,6 02 ,24 ,15 PQv Recall that the parametric e quations of a line are given by tczztbyytaxx000 , ,. We can use either point P or Q as our point on the line ) ,,(000zyx. We choose the point P and assign ) 0,2,1(),,(000zyx. The terms a, b, and c are the components of our parallel vector given by v = < -6, 2, 2 > found above. Hence a = -6, b = 2, and c = 2. Thus, the parametric equati on of our line is given by (2) 0 ,(2) 2 ),6( 1tztytx or tt, zytx222 ,61 To find the symmetric equations, we solve each parametric equation for t. This gives 2 ,22 ,61ztytxt Setting these equations equal gives the symmetric equations. 22261zyx The graph on the following page illustrates the line we have found
PAGE – 6 ============
6 It is important to note that the equations of lines in 3D space are not unique. In Example 2, for instance, had we used the point Q = (-5, 4, 2) to represent the equation of the line with the parallel vector v = < -6, 2, 2 >, the parametric equations becomes tt, zytx2224 ,65
PAGE – 8 ============
8Planes in 3D Space Consider the plane containing the point ) ,,(000zyxP and normal vector n = < a, b, c > perpendicular to the plane. The plane consists of all points Q = (x, y, z) for which the vector PQ is orthogonal to the normal vector n = < a, b, c >. Since PQ and n are orthogonal, the following equations hold: 0PQn 0,,000zzyyxxcba 0)()()(000zzcyybxxa This gives the standard equation of a plane. If we expand this equation we obtain the following equation: 0Constant 000dczbyaxczbyax x y ),,(000zyxP ),,(zyxQz n = < a, b, c >
PAGE – 9 ============
9Setting 000czbyaxd gives the general form of the equation of a plane in 3D space 0dczbyax. We summarize these results as follows. Standard and General Equations of a Plane in the 3D space The standard equation of a plane in 3D space has the form 0)()()(000zzcyybxxa where ),,(000zyx is a point on the plane and n = < a, b, c > is a vector normal (orthogonal to the plane). If this equation is expanded, we obtain the general equation of a plane of the form 0dczbyax Note!! To write the equation of a plane in 3D space, we need a point on the plane and a vector normal (orthogonal) to the plane.
44 KB – 18 Pages